System_dwókowy

Szczegóły

Odsłony: 5276

Dwójkowy system liczbowy lub też system binarny (NKB – naturalny kod binarny) – pozycyjny system liczbowy, którego podstawą jest liczba 2, a do zapisu liczb potrzebne są tylko dwie cyfry: 0 i 1

Używany jest głównie w informatyce, stanowi bowiem język, jakim posługują się komputery. Każdy program komputerowy - niezależnie od tego w jakim języku programowania napisany - ostatecznie zostaje tak czy inaczej "przetłumaczony" na ciąg zer i jedynek, a zatem zapis w systemie binarnym.

Dlaczego komputerowi taki system?

    Komputer zbudowany jest z części elektronicznych. Przekazywanie informacji pomiędzy poszczególnymi elementami w komputerze polega na odpowiednim przesyłaniu sygnałów. Podstawą elektroniki jest prąd elektryczny, który w układach elektronicznych albo płynie albo nie. Zatem, aby łatwiej było komputerowi rozpoznawać sygnały, interpretuje on płynący prąd jako "1" (jeden), a jego brak jako "0" (zero). Nie trudno się domyślić, że komputer operując odpowiednim ustawieniem, kiedy ma płynąc prąd, a kiedy nie ustawia różne wartości zer i jedynek. Procesor konwertuje je na liczby i w ten sposób powstają czytelne dla nas obrazy, teksty, dźwięk itd.

  WAŻNE!!!

1. Komputer widzi tylko zera i jedynki.

2. Bity przyjmują tylko jedną z tych dwóch wartości 0 lub 1

3. 1Bajt = 8 bitów (Osiem bitów to jeden bajt)

4. Ustawienie ośmiu bitów decyduje o numerze, który może przyjąć maksymalnie 256. Numer decyduje o znaku, jaki komputer ma wykorzystać.

JAK ZAMIENIĆ LICZBĘ W SYSTEMIE DZIESIĘTNY NA DWÓJKOWY I ODWROTNIE?

OTO JEST PYTANIE?

  ZAMIANA - SYSTEM DZIESIĘTNY NA DWÓJKOWY (10 na 2)

 System dziesiętny

W naszym życiu i w zakresie matematyki wychowaliśmy się na systemie dziesiętnym. System dziesiętny to system liczbowy zwany systemem arabskim. W tym systemie do zapisu liczby używamy cyfr 0 1 2 3 4 5 6 7 8 9, w którym każda pozycja cyfr składających się na liczby jest określona kolejną potęgą dziesiątki (a po prawej stronie są cyfry z najmniejszą wagą pozycji).

Na przykład liczba 3458 przedstawiona w systemie dziesiętnym to będzie:

3*1000+5*100+4*10+8*1 = 3548

3*10³+5*10²+4*10¹+8*10⁰ = 3458

Innymi słowy każdą liczbę w systemie dziesiętnym możemy zapisać przy pomocy sumy iloczynów potęg liczby 10.

Konwersja (jak podaje słownik PWN to - przekształcenie postaci czegoś)

czyli my zamieniamy postać liczby dziesiętnej na dwójkową (binarną) 

  Sposób jest następujący:

1. Bierzemy np. liczbę 6

2. Liczbę  6 dzielimy przez 2 i jeżeli wynik będzie z resztą: zapisujemy 1, jeżeli nie - zapisujemy 0.

3. Następnie znowu dzielimy przez 2 to co zostało z liczby, ale bez reszty.

4. Wykonujemy działania, aż zostanie 0 (zero).

5 Otrzymane zera i jedynki zapisujemy w odwrotnej kolejności. Od dołu do góry

Co daje 110.

    Widzimy, że zawsze na samym końcu po podzieleniu będzie 0, zatem ostatnia liczba jest równa 1.  Co za tym idzie - pierwsza cyfra w zapisie dwójkowym jest ZAWSZE RÓWNA 1.  Przyjęliśmy bowiem, że dla komputera brak przepływu prądu oznacza "0", natomiast przepływ prądu - "1". Sygnał zatem nie może zaczynać się od "0", gdyż jest to brak sygnału (brak napięcia). Procesor nie wie, czy sygnał już się zaczął, czy jeszcze nie. Początek musi być "1" (jest sygnał). 

 Zamieńmy liczbę 40 na system dwójkowy

I jeszcze jeden przykład liczba - 63

I ostatni przykład - liczba 25

 ZAMIANA - SYSTEM  DWÓJKOWY NA DZIESIĘTNY (2 na 10)

 Konwersja polega na dodawaniu iloczynów kolejnych potęg dwójki i odpowiadającym im cyfr z liczby binarnej.

To znaczy? Zamienńmy liczbę 110

1. Nad liczbą dwójkową oznacz poszczególne potęgi zaczynając od 0 z prawej strony.

2. Następnie weź pierwszą cyfrę z liczby dwójkowej i pomnóż ją przez 2 podniesione do potęgi oznaczonej u góry ( w naszym przykładzie to będzie)

- kolor czarny

- kolor czerwony

- kolor niebieski

3. Następnie podnieś do potęgi, pomnóż i dodaj. Otrzymasz wynik 6

Jeszcze jeden przykład. Zamieńmy liczbę 11111 na liczbę w systemie 10

1. Zaczynamy od wpisania potęg nad liczbą dwójkową

2. Następnie dodajemy iloczyny kolejnych potęg dwójki i odpowiadającym im cyfr z liczby binarnej.

3. Wykonujemy działania matematyczne 

 Zadanie 

Zamień liczbę  dwójkową 1110001 na dzisiętną

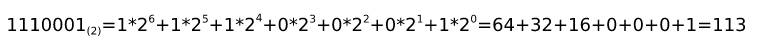
Jaka to numer telefonu?

Odpowiedż prześlij na adres: Ten adres pocztowy jest chroniony przed spamowaniem. Aby go zobaczyć, konieczne jest włączenie obsługi JavaScript. wpisując w temat listu - system dwójkowy

Zobacz świetny kalkulator, który zamienia liczy dziesiętne na dwójkowe i dwójkowe na dziesiętne.  >> KALKULATOR <<